Mitä yhteistä on ensimmäisen kierroksen voittaneella mäkihyppääjällä, vuoden pahimmalla liikenneonnettomuuspaikalla, koululaisen huonolla koesuorituksella ja tuotteella, jonka bränditulos näyttää poikkeuksellista nousukiitoa?
Tyypillisesti käy niin, että johtava mäkihyppääjä yleensä hyppää toisella kierroksella merkittävästi huonommin (jonka selostajat panevat herkästi hermojen piikkiin). Onnettomuuspaikalle asennetaan liikennekamera - ja seuraavana vuonna onnettomuudet dramaattisesti vähenevät. Nuhtelua saanut koululainen parantaa tulostaan ja tuotteen huima nousukiito maltillistuu merkittävästi.
Näiden esimerkkien ilmiö on nimeltään "paluu keskiarvoon", (regression to the mean). Käsitettä käytti ensi kerran yleisnero (ja mm. kyselytutkimusten pioneeri, korrelaation ja regression käsitteiden kehittäjä) Sir Francis Galton 1800-luvulla huomattuaan, että vanhempien äärimmäiset ominaisuudet, kuten poikkeuksellinen pituus tai älykkyys, eivät periytyneet täysin jälkeläisilleen. Poikkeuksellisen pitkien vanhempien lapset - vaikka olivat kyllä keskimääräistä pitempiä - eivät tyypillisesti olleet kuitenkaan niin pitkiä kuin vanhempansa vaan heidän pituutensa lähestyi koko väestön keskiarvoa. Ilmiö johtuu täysin satunnaisuuden luonteesta, vaikka virheelliset kausaaliset selitykset ovatkin hyvin tyypillisiä.
Palatakseni esimerkkeihin:
Mäkihyppy: Ensimmäisen kierroksen voittanut mäkihyppääjä on epäilemättä taitava, mutta hänen äärimmäinen menestyksensä johtui myös mm. suotuisista tuuliolosuhteista. Koska taidot pysyvät vakaina, mutta olosuhteet vaihtelevat hyppyjen välillä, todennäköisyys saada yhtä täydelliset olosuhteet seuraavalla kierroksella on pienempi. Tämä voidaan tiivistää yhtälöön: [äärimmäisen hyvä lopputulos] = [äärimmäisen hyvät taidot] + [äärimmäisen hyvä tuuri]. Jos olet heittänyt nopalla kutosen, todennäköisyys heittää uudelleen vähintään yhtä hyvin on pienempi kuin jos olisit ensin heittänyt kolmosen.
Liikenneonnettomuudet: Vuoden pahimmaksi onnettomuuspaikaksi valikoituu paikka, joka on luonnollisesti vaarallinen, mutta äärimmäinen tulos johtuu myös satunnaisista olosuhteista, kuten sen vuoden keliolosuhteista. Liikennekameran asennuksen jälkeen havaintaan vähemmän onnettomuuksia, mutta koska äärimmäinen tulos lähestyy joka tapauksessa keskiarvoa, pelkästään onnettomuuksien vähenemisen perusteella ei voida päätellä kameran olleen tehokas.
Koululaisen koetulos: Jos koululainen saa omaan tasoonsa nähden huonon koetuloksen, vanhempi luonnollisesti antaa herkästi nuhtelevaa palautetta tai pyrkii korjaamaan opiskeluprosessia. Ongelma ei ole siinä, että tämä ei toimisi vaan nimenomaan siinä, että se lähes varmasti toimii! Äärimmäisen huono koetulos paranee seuraavalle kerralle melkein varmasti. Tämä pätee valitettavasti myös kääntäen: jos koetulos onkin poikkeuksellisen hyvä, kehut ja positiivinen palaute näyttää vetävän koemenestystä alaspäin, koska äärimmäisen tuloksen mahdollistanut hyvä tuuri (esim. sopivat kysymykset) ei enää toistunut. Tietämättömyys paluusta keskiarvoon tuomitsee vanhemman oppimaan, että positiivinen palaute on haitallista ja negatiivinen toimivaa.
Ilmiö näkyy kaikissa prosesseissa, joissa on satunnaiskomponentti (joita ovat jotakuinkin kaikki tosielämän prosessit). Ja jos prosessissa on mikään merkittävä määrä satunnaisuutta, sen tuottamat äärimmäisyydet johtuvat suurella todennäköisyydellä sattumasta. Vaikutus on myös sitä suurempi, mitä suurempi satunnaiskomponentin osuus on.
Markkinatukimuksessa ja erityisesti tracker-tyyppisissä jatkuvissa tutkimuksissa ilmiö tulee vastaan jatkuvasti kun mitattavia tuotemerkkejä ja mittareita on paljon. On luonnollista innostua odotuksiin nähden poikkeuksellisen hyvästä brändituloksesta ja reagoida poikkeuksellisen huonoon tulokseen toimenpiteillä. Tässä kuitenkin piilee sama väärintulkinnan riski, kuin aiemmissa esimerkeissä: esimerkiksi reagoimalla huonoon äärimmäisyyteen paniikkimarkkinoinnilla tai hintakampanjalla näkee vaikutuksia liiankin helposti, vaikka todellisuudessa kyseessä olisi vain paluu keskiarvoon.
Seuraavassa kuvassa meillä on simuloitua aikasarjadataa, joka kuvaa jotain seurattavaa mittaria. Datassa ei ole todellista trendiä, mutta siihen on lisätty satunnaisvaihtelua (oikeassa mittauksessa satunnaisuuden lähteitä ovat mm. näytteen koko, mahdolliset muutokset koejärjestelyssä, kutsujen lähetysajat ja -päivät ym. ym. - tämän lisäksi myös itse mitattavassa asiassa voi olla ja aina onkin satunnaiseksi tulkittavaa vaihtelua).
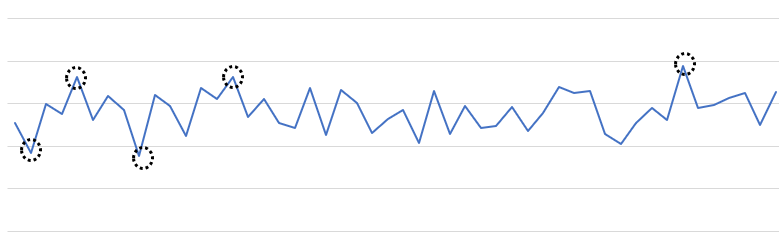
Kaikki äärimmäiset tulokset - siihenastiset ennätykset - on merkitty. Ja kuten näkyy, jokaisessa tapauksessa ennätystä seuraava mittaus on tuottanut vähemmän äärimmäisen tuloksen.
Ilmiö säilyy, vaikka lisäämme mittariin päivänselvän trendin ylöspäin.
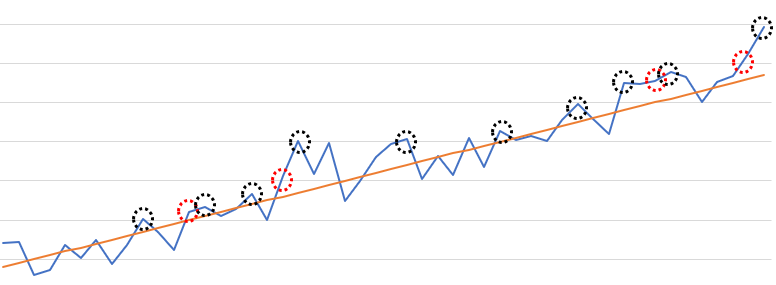
Äärimmäisen huonoja tuloksia ei enää ole, mutta tässäkin tapauksessa, jossa trendi on selvä, äärimmäisen hyviä tuloksia seuraa huonompi 11/14 tapauksessa. On myös huomionarvoista että äärimmäiset tulokset ovat niitä kaikkein virheellisimpiä, eli ne poikkeavat eniten todellisuudesta (punainen viiva). Myös 100% niistä on biasoituneita ylöspäin (eli niissä on plusmerkkinen virhe).
Miten tähän pitäisi suhtautua? On tärkeää ymmärtää, että vaikka ennätystulos onkin signaali hyvästä tilanteesta, tilanne ei todennäköisesti ole niin hyvä kuin signaali antaa ymmärtää. Yksittäisen tuloksen tulkinnassa on oltava varovainen.
Suositukset:
1. Älä vedä johtopäätöksiä yksittäisestä tuloksesta. Yksittäistä lukua tai muutosta ei pitäisi tulkita todellisuudeksi - oikeastaan lähes koskaan. Odota seuraavaa kierrosta tai tarkastele myös menneitä tuloksia. Monen riippumattoman tuloksen muodostama trendi on yleensä luotettavampi tulos kuin yksittäinen rajukin muutos.
2. Yritä löytää riippumatonta tietoa vahvistamaan havainnot. Toinen datalähde tai jopa asiantuntijan valistunut arvaus vahvistaa tulosta kunhan se on tuloksesta riippumaton.
3. Vältä jälkikäteisiä selityksiä. Syiden etsiminen äärimmäisille tuloksille jälkikäteen ei ole hedelmällistä, koska satunnaiskomponentin osuus tuloksessa voi olla hyvin suuri. Tämä johtaa myös helposti ns. vahvistusharhaan, jossa etsitään vain niitä tosiasioita, jotka tukevat havaintoa ja jätetään huomiotta ne, jotka ovat sen kanssa ristiriidassa.
Yhteenvetona:
Paluu keskinkertaisuuteen on tilastollinen ilmiö, jossa äärimmäistä mittusta seuraa maltillisempi.
Tämä johtuu siitä, että äärimmäisessä tuloksessa on todennäköisesti myös äärimmäinen satunnaiskomponentti.
Reagointi ääritulokseen voi luoda illuusion, että toimenpiteet ovat tehokkaita silloinkin kun ne eivät sitä ole.
Äärimmäisiin tuloksiin tulee suhtautua skeptisesti ja etsiä lisäevidenssiä ennen johtopäätösten vetämistä.